Hypergeometric Samples
Once a month, a random sample (of size n) is chosen from a population (of size M). This population might be of student-athletes for NCAA drug-testing, or taxpayers for audit, or some other similar scenario. How likely is it that there will be x repeats from one month to the next month? This is a useful question to ask, as it can help point out systematic problems in the sampling process. Student-athletes, in the hypothetical situation, might be annoyed that they are called for drug-testing many times in a row. Or it might point to the unjust use of the tax audit process for political reasons (assuming, of course, that the tax system could be just at all).
Let's start by trying to characterize this problem. It is a discrete problem, as we are not looking at fractional people. The population size is finite (say, M=700). The sample size may be significant (say, n=40). The individual objects do not matter (i.e. we are concerned if a particular person is chosen twice in a row, but rather that ANY person is chosen twice). We are selecting objects without replacement from the population (i.e. nobody can be chosen twice within a month).
This class of problem actually has a closed-form analytic solution, using the hypergeometric distribution. Consider the second month: There are 40 objects (n) that had been chosen in the previous month and might potentially be chosen this month. (I think of them as red marbles, with the rest of the population being blue marbles. But maybe I'm just weird.) The first time we choose one of the objects, the probability of choosing one of the original 40 is 40/700. The next time we choose an object, the probability has changed, because we have already pulled an object from the population. (If the first selection was one of the last month's group, then the probability that the next would be is 39/699.) And so on, through, the 40th trial. If you multiply out those combinations, then you will have the hypergeometric distribution function (shown below, image from the Mathworks website).
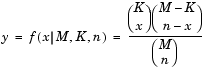
It is also possible to simulate the problem, using a Monte-Carlo approach. This requires many many random trials, but can be done fairly easily using a computer. I used one million trials, and the results match closely to the analytical solution. I programmed it with C# on Microsoft's Visual Studio. It took less than five seconds to run, on my Pentium 4 2.8 GHz laptop. (I didn't even bother to use a release build, which may make things a bit faster.) The (trivial) source code is available here. (Some people have done some tests of the .Net random number generator, available here.)
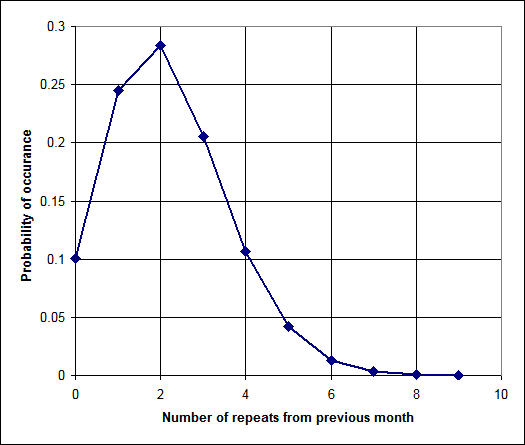
The results can be seen the graph below (n=40, M=700). The average number of repeats per month is 2.2, with the probability of 0.1% for eight or more repeats in a given month. A good practice would be to record the number of repeats each month. After several months, the recorded results should look similar to the graph, unless the selection process is not random (or some other assumption, such as the population or sample size, are violated).
Thanks to Dave Loeffelholz and Dr. Richard Stern for the insights into the problem.
Comments
Jeffy-I don't think there is any question that you are weird. But thank you for clearing up a problem that has been keeping me up most nights....Cool analysis. I actually read one of your entries that didn't include pictures.-Emmy
Posted by: Emily | September 22, 2004 11:38 AM
Jeff - for kicks, you might like to try a well-documented brain teaser along the same lines:
What is the probability that two or more children in a classroom of 30 share the same birthday? (For simplicity, assume all children were born in the same calendar year and assume a uniform probability distribution of birthdays)
The answer is surprisingly high.
Posted by: Dave | September 22, 2004 05:33 PM